A Statistical Appraisal Of Bond And Equity Behaviour
- Peter Elston

- Aug 22, 2022
- 6 min read
If you enjoy reading this blog, please post a review on WealthTender. Thank you!
Bonds and equities exhibit fundamentally different patterns
I have just updated a dataset of monthly real returns from US stocks - equities - and US bonds going back to January 1850, then rerun some old analyses on the data as well as some new ones. This post simply presents the results of the analyses. In another post I will set out what I think are the implications of them. Suffice to say, much of the conventional wisdom about these two main asset classes is flawed.
First off, all returns have been adjusted for inflation. Nominal returns are utterly irrelevant and always will be. What use is a 10% nominal return if goods and services prices have risen 20%?
Also, to be clear, bonds are long maturity - as opposed to bills - and are high grade/have very low default risk - as opposed to credit.
Charts 1 and 2 below are simply of the inflation adjusted equity and bond indices on semilog scales.
What I find extraordinary about US equities is that despite underlying economic growth having gradually declined as the US economy matured, the trend real growth in US equities has not wavered. If economic growth gradually fell, corporate revenue growth should also have fallen, in which case one might have expected equity trend growth to fall. It didn't.
One can derive the trend growth rate from the trend line formula on the chart. Since the data is monthly, the exponent constant of 0.005189 means that trend monthly growth is 0.5189pct which equates to 6.4pct annualised.
Trend real growth in bonds can be derived from the trend line formula in Chart 2. Trend monthly growth of 0.1778pct equates to 2.2pct annualised.
Equities have gone up far more than bonds over the 172 years so to compare like with like I have put them together in Chart 3.
Chart 1:
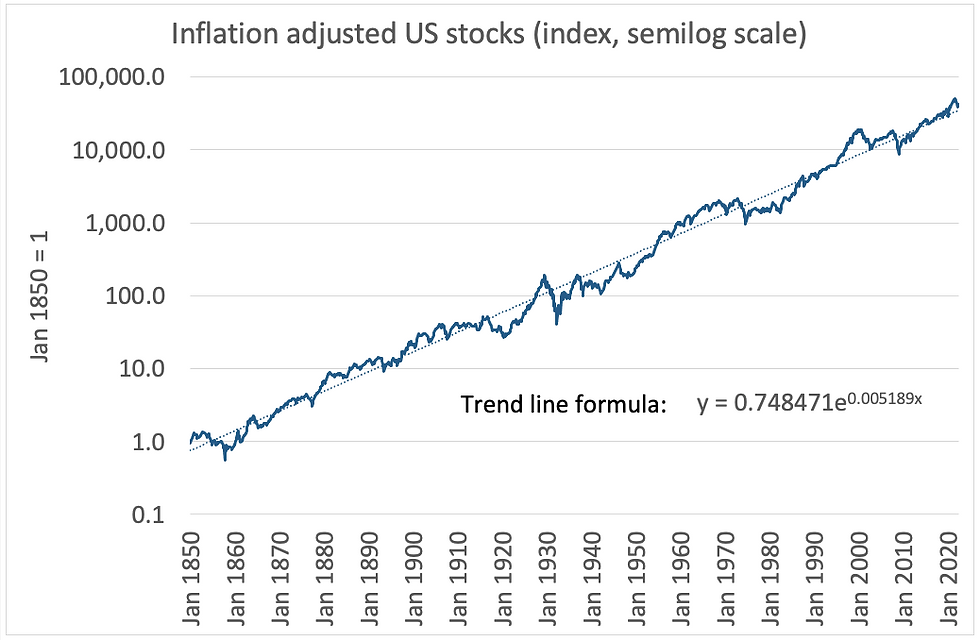
Source: Credit Suisse/Yahoo
Chart 2:
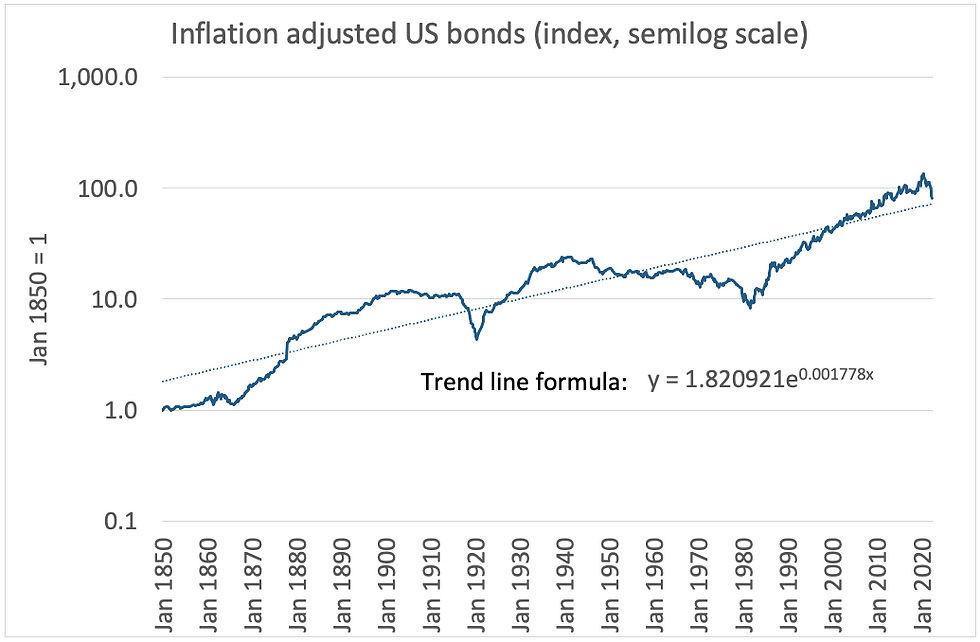
Source: Credit Suisse/Yahoo
Chart 3 clearly shows that equities have performed much better than bonds over the 170 years - the difference between 6.4pct and 2.2pct per annum. It should also be noted that the bonds' line is less jagged than equities', and also that it contains three distinct cycles that equities' line does not.
Chart 3:
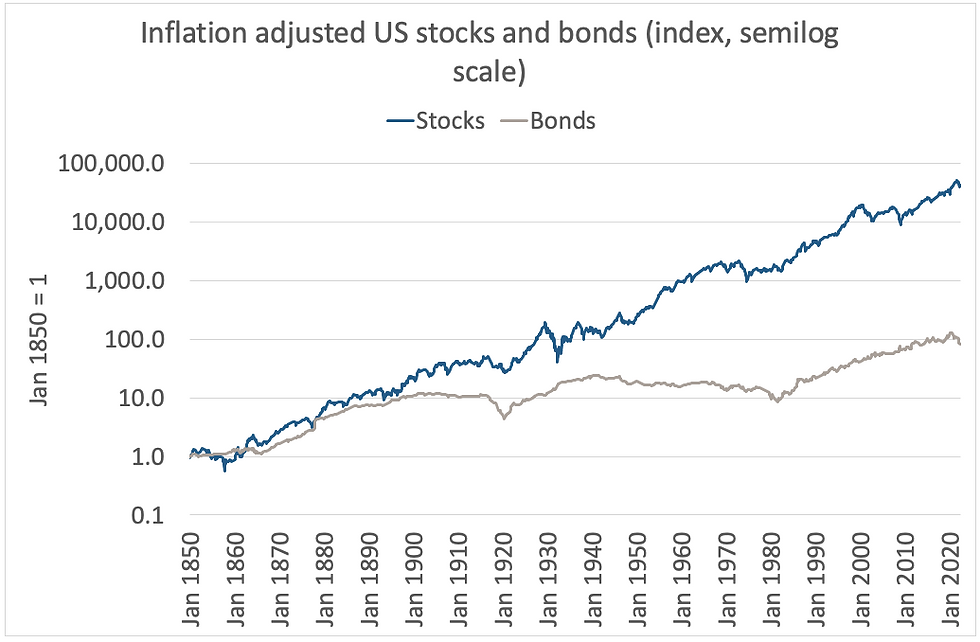
Source: Credit Suisse/Yahoo
Charts 4 and 5 are normalised indices, derived by dividing the actual index by the trend line - another term for normalised is de-trended. Thus a value of 2 means that the index is 100% above trend and 0.5 means 50% below. The chart is semilog because doubling - 2.00/100% - is equivalent to having - 0.50/50%. If you double something - +100pct - then halve it - -50pct - you get back to where you started, not to 100pct-50pct = +50pct.
Note that the jaggedness/cycles are now even more apparent in the two charts.
Chart 4:
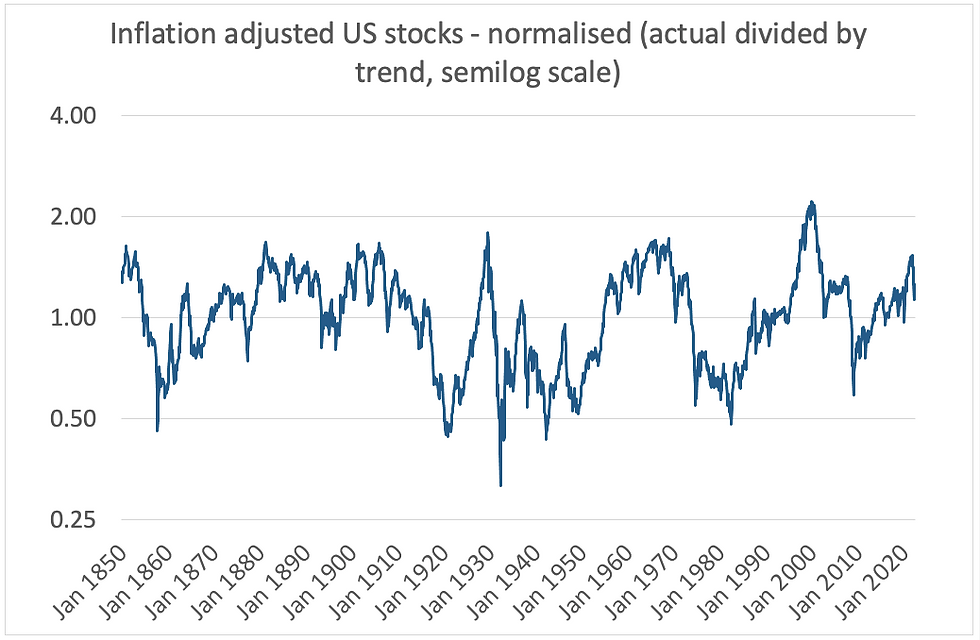
Source: Credit Suisse/Yahoo
Chart 5:
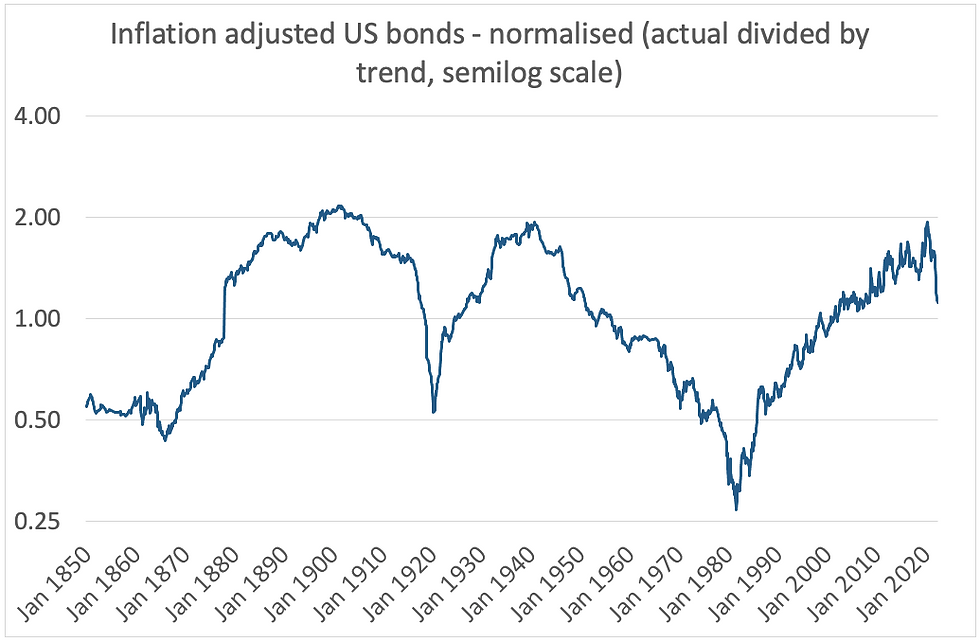
Source: Credit Suisse/Yahoo
Charts 4 and 5 are overlain in Chart 6 below. You would be forgiven for thinking that there might just be some correlation between the two. They both reach lows in around 1860/70, 1920, and 1980, as well as highs around 1900 and, perhaps more tenuously, 2020. In fact the correlation coefficient between them, R, is 0.16 which is low - Chart 7.
It is also instructive that the range for both series is around 0.50 to 2.00, though each has one excursion towards 0.25, i.e. towards 75% below trend.
Chart 6:
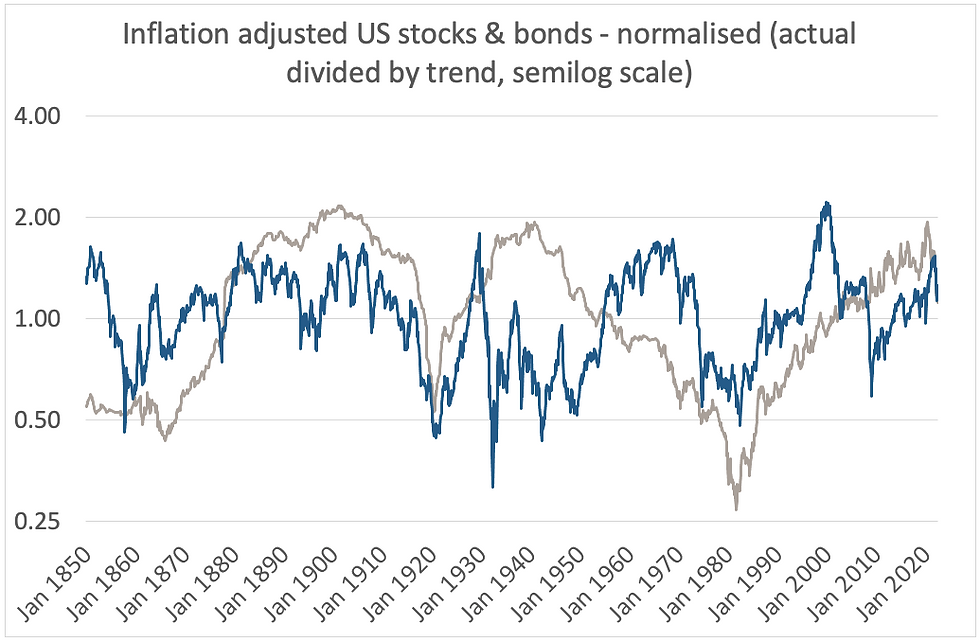
Source: Credit Suisse/Yahoo
While the correlation coefficient, R, between bonds and stocks over the entire 170 years is a low 0.16, there are fairly long periods - 20 years - when there is a high degree of correlation, whether positive or negative. For example, 1900-1920 saw both real stocks and bonds falling - a high, positive correlation coefficient of 0.90 - while 1948-1968 saw stocks falling and bonds rising - a "high", negative correlation coefficient of -0.89.
Periods can generally be classified into five groups: both are rising; both are falling; one is rising and the other falling; one is falling and the other rising; and, finally, no obvious relationship. Which of these is prevalent depends largely on the underlying economic/inflation regime.
Chart 7:

Source: Credit Suisse/Yahoo
The behaviour of financial assets, whether bonds or equities, individual names or markets, is generally defined by two parameters: average return, and standard deviation of returns. If you plot a histogram of returns you will get something close to a bell curve, with the average return in the centre.
If the financial asset follows a random walk, 68pct of the returns will be within one standard deviation on the mean, 95% within two, 99.7pct within three, etc.
In the case of equities, we already know that the average monthly return over the 172 years is 0.52pct. To calculate the standard deviation, one must first take logarithms to remove skew - think of a wonky bell curve - then convert back.
Once you have a mean and standard deviation, you can create simulations of time series of financial asset prices, ones that follow a random walk.
Charts 8 below depicts 100 randomly selected actual 30 year equity market periods. Chart 9 depicts 100 simulations based on mean and standard deviation based on actual monthly returns. The red lines represent +1 and -1 standard deviations.
As you would expect from the random walks in Chart 9, many of the series lie outside +/-1 standard deviation. In Chart 8 however, this is not the case. The difference between the two charts is stark - remember that the vertical scales are the same. A number of the actual series in the early years do veer outside of +/- 1 standard deviation but then they are drawn back inside the red lines.
Charts 10 and 11 are exactly the same but for bonds. Again, there is a difference between the two - the actual series veer farther from the mean than the simulations. This is the opposite to the pattern seen in equities.
Chart 8:
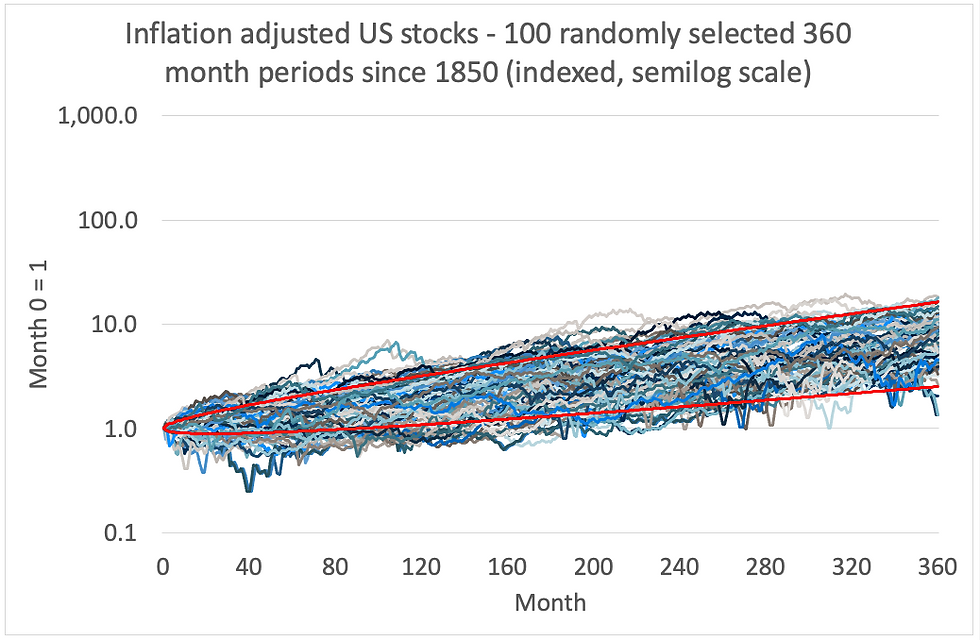
Source: Credit Suisse/Yahoo
Chart 9:
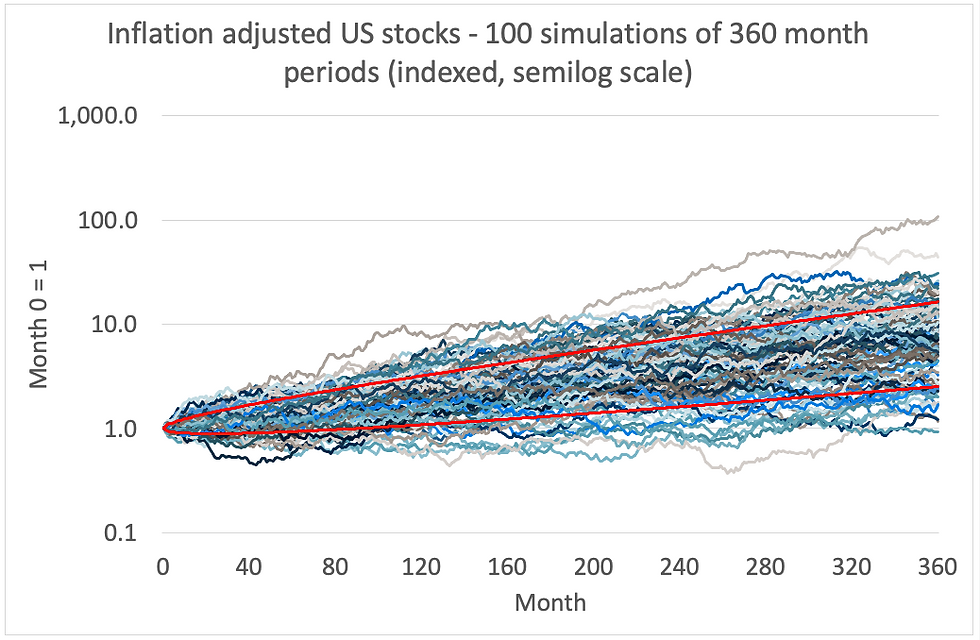
Source: Credit Suisse/Yahoo
Chart 10:
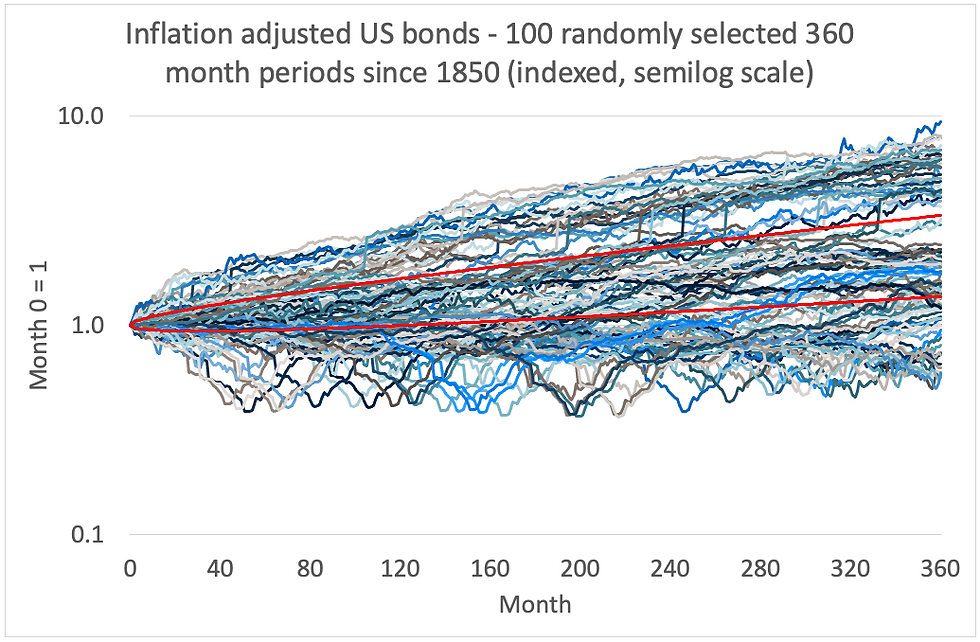
Source: Credit Suisse/Yahoo
Chart 11:

Source: Credit Suisse/Yahoo
Just by eyeballing Charts 8 and 10 it is clear that neither bonds nor equities follow a random walk. However, there is a mathematical test called the variance test that can quantify the extent of the non-randomness. Essentially, if a series follows a random walk, the variance of 4 month returns should be double the variance of 2 month returns, 10 month double 5 month, etc. Dividing the variance over, say, 9 months by 9, then dividing it by the variance over 1 month, should give you a value close to 1 if over 9 month periods the time series is following a random walk.
Charts 12 and 13 below show actual/simulated variance ratios for, respectively, equities and bonds. As expected, the variance ratios for both simulated series are close to 1, indicating that they are following random walks. Not so with the actual equities and bonds.
In the case of equities, they start off being more volatile than would be expected, then over longer periods get progressively less so. In the case of bonds, they are immediately more volatile over short periods, then become even more so over longer ones.
The two actual series are plotted together in Chart 14. The difference I think is extraordinary, and demonstrates the almost fundamentally different nature of these two main asset classes.
Variance is simply the square of standard deviation, so one can create series of standard deviation of actual returns over a particular number of months, then plot them on a chart. This is what is depicted in Chart 15, the final chart.
One would naturally expect the volatility of, say, 10 year returns to be higher than that of, say, 6 month returns - in other words, both lines on the whole are moving up. Equities get more volatile in relation to bonds over shorter periods, but then around 3 years the gap starts to narrow. This gap continues to narrow until the ten year mark, at which point equities become less volatile than bonds. Thereafter, the gap between bond volatility and equity volatility continues to widen. In other words, over longer periods bond returns are much more volatile than those from equities.
As I will expand upon in another post this week, this is a fascinating and counterintuitive finding. Patterns in markets mean that there are opportunities to make predictions and thus to outperform. The difference in patterns between equities and bonds highlighted in this post provide further knowledge about these two key asset classes which can provide further scope for outperformance.
Chart 12:
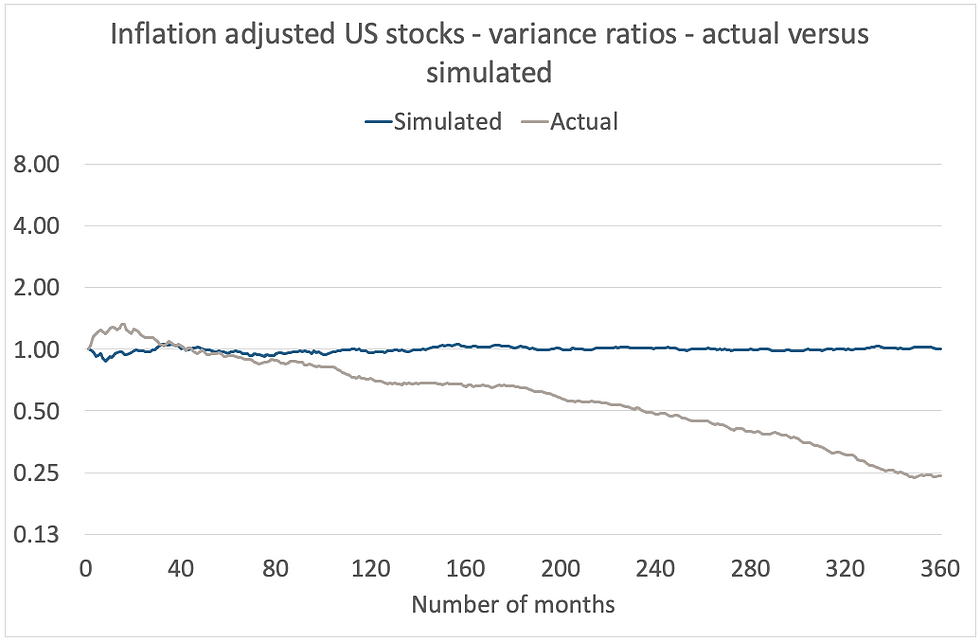
Source: Credit Suisse/Yahoo
Chart 13:

Source: Credit Suisse/Yahoo
Chart 14:

Source: Credit Suisse/Yahoo
Chart 15:
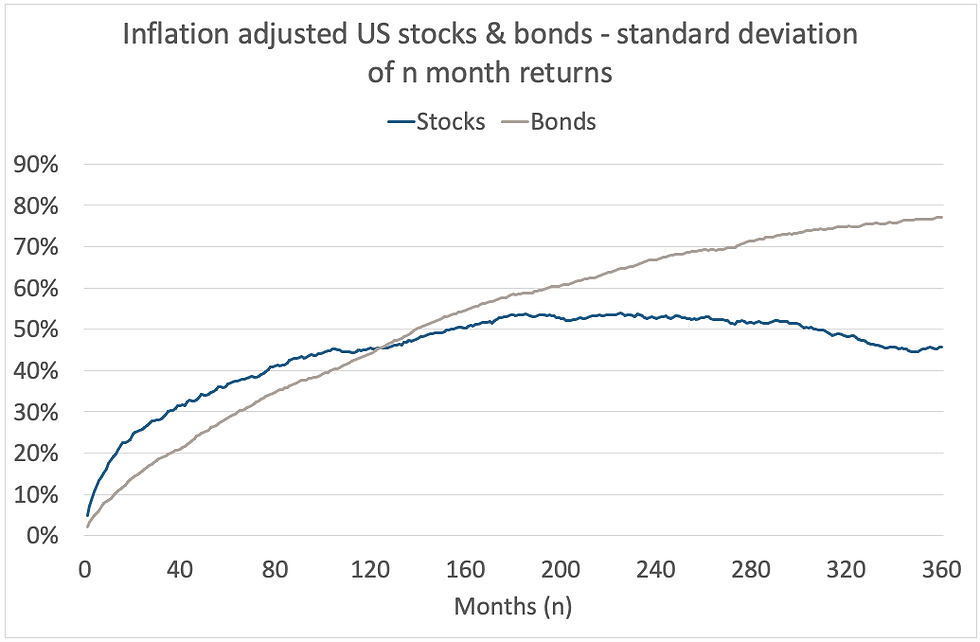
Source: Credit Suisse/Yahoo
The views expressed in this communication are those of Peter Elston at the time of writing and are subject to change without notice. They do not constitute investment advice and whilst all reasonable efforts have been used to ensure the accuracy of the information contained in this communication, the reliability, completeness or accuracy of the content cannot be guaranteed. This communication provides information for professional use only and should not be relied upon by retail investors as the sole basis for investment.
© Chimp Investor Ltd




Comments